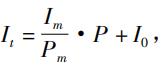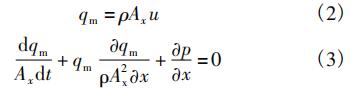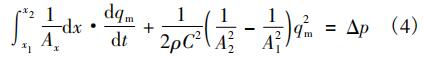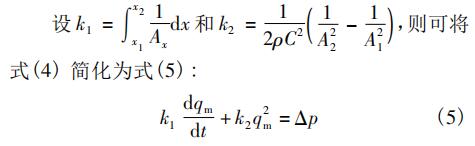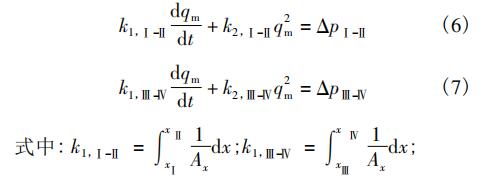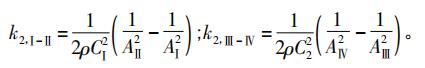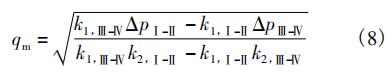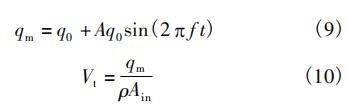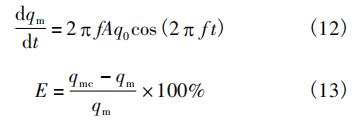1引言

        差壓式流量計［1］一般以孔板、文丘里管、噴嘴或其它形式的節流元件形成差壓，進而計算流體流量。差壓式流量計由于其結構簡單、無可動部件等特點而廣泛應用于測量封閉管道中單相穩定流體的流量，常用于測量空氣、天然氣、水等流體的流量。差壓式流量計是非常為傳統且應用廣泛一種流量測量裝置，該類流量計的準確測量是以平穩流動為基礎，當測量流體壓力、速度隨時間呈周期變化情形時，以穩態流的計算方法直接求取脈動流量將因遺漏流量導數項而引起較大測量誤差［2～4］。而脈動流廣泛存在于工業管路中，由于旋轉式、往復式或可運動傳送設備的使用，管道中流量控制設備的周期振蕩，以及流程中工藝設備的特定要求，眾多因素都會導致流體產生脈動流［5～8］。ISO5167中明確規定差壓式流量計不適用于脈動流的測量。

 

        本文以經典文丘里管［9］為研究對象，通過FLUENT軟件［10］對文丘里管在正弦脈動流下的流場進行仿真計算，分析了單路差壓計算脈動流量時由導數項引入的測量誤差，提出了基于雙路差壓的脈動流量測量方法，并利用仿真結果證明該方法的有效性。

 

2脈動流量計算方法

2．1脈動流理論模型

        在脈動流狀態下，假設流體流過節流件為一維流動［11，12］，流量計內流動運動方程為:

        由于質量流量qm可由式(2)表示，則式(1)可進一步表示為式(3)。

        式中Ax為x處管道橫截面積。

 

        假設節流件上游取壓孔處于截面1位置，坐標為x1;下游取壓孔處于截面2位置，坐標為x2;在截面1和截面2之間沿流線對式(3)進行積分，可得:

 

        式中:A1和A2分別是截面1和截面2的截面積;Δp為截面1和截面2之間壓差;C為節流件流出系數。

2．2雙路差壓流量計算方法

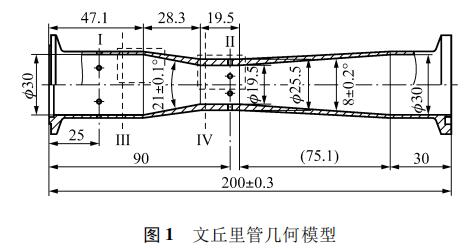
        在實際情況中流量導數項無法確定，傳統的通過兩截面之間單路差壓計算流量的方法無法計算瞬時脈動流量，可通過測量兩對截面之間雙路差壓，消除流量導數項的影響，進而計算瞬時脈動流量。在收縮段前后各取2個截面，分別定義為截面Ⅰ、截面Ⅱ、截面Ⅲ和截面Ⅳ，如圖1所示。4截面沿軸向的坐標分別是xⅠ、xⅡ、xⅢ和xⅣ。截面Ⅰ與截面Ⅲ內徑相同，截面Ⅱ和截面Ⅳ內徑相同，截面Ⅰ和截面Ⅱ之間流出系數為C1，截面Ⅲ和截面Ⅳ之間流出系數為C2。

        在截面Ⅰ和截面Ⅱ之間，截面Ⅲ和截面Ⅳ之間具有如式(6)和式(7)所示關系。

        聯立式(6)和式(7)，消除流量導數項，可得質量流量與雙路差壓的函數:

 

 

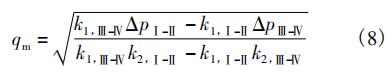
3、流體仿真驗證

3．1幾何模型

        本文以文丘里管為對象，利用FLUENT軟件進行流體仿真，獲得兩對截面間雙路壓差，對脈動流量計算方法進行驗證。圖1所示的文丘里管進出口內徑D=?30mm，喉徑d=?19．5mm，直徑比β=0．65，以進口截面中心為坐標原點，截面Ⅰ、截面Ⅱ、截面Ⅲ和截面Ⅳ這4截面坐標分別是xⅠ=25mm、xⅡ=90mm、xⅢ=46mm和xⅣ=78mm。

 

3．2流體仿真模型

        利用ICEM軟件進行幾何建模，忽略重力因素影響，基于文丘里管內流場軸對稱特性，建立二維軸對稱幾何模型并進行網格劃分。文丘里管上游設置10倍長直管段，下游設置5倍直管段。仿真模型壁面設置5層邊界層網格，中心區域為三角非結構化網格。

 

        仿真中選用標準k-ε湍流模型，選用液體水作為流體介質。設置下游直管段出口為自由出流條件，直管段及文丘里管壁為靜止壁面;上游直管段入口為速度入口，通過UDF函數定義，可計算得到入口流速。

        式中:qm為瞬時質量流量，kg/s;q0=2kg/s為質量流量平均值;A為脈動幅度;f為脈動頻率;t為運行時間，s;Vt為瞬時入口速度平均值，m/s;ρ為流體密度，kg/m3;Ain為上游直管段入口截面積，m2。

 

3．3單路差壓流量計算誤差

        由穩態流動下仿真結果，可獲得截面Ⅰ和截面Ⅱ之間流出系數C1=0．9815，截面Ⅲ和截面Ⅳ之間流出系數C2=1．007。進一步可獲得k1，Ⅰ-Ⅱ=141．75，k2，Ⅰ-Ⅱ=4788．9，k1，Ⅱ-Ⅲ=71．856，k2，Ⅲ-Ⅳ=4549．4。

 

        穩態流動下，質量流量qmc可由式(11)計算:

        正弦脈動流情況下，流量導數可由式(12)表示，若直接通過式(11)計算瞬時質量流量引入的導數項誤差通過式(13)計算:

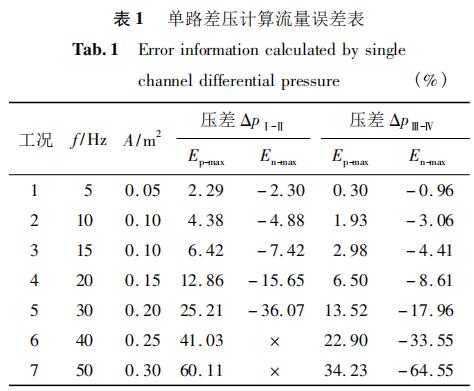
        表1所示為7個工況單路差壓計算流量誤差數據。其中Ep-max表示誤差上限，En-max表示誤差下限。

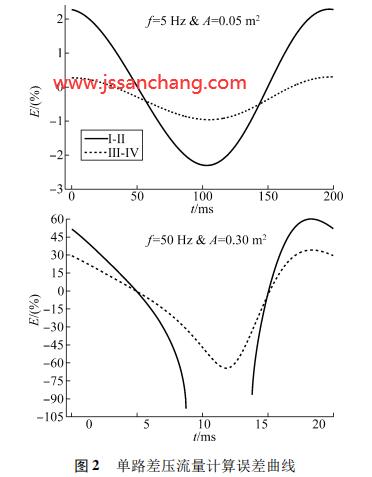
        圖2是工況1和工況7單路差壓流量誤差曲線。表1中“×”位置和圖2(b)中曲線中斷處是由于ΔpⅠ-Ⅱ為負值造成。通過ΔpⅠ-Ⅱ和ΔpⅢ-Ⅳ計算瞬時流量，對應時刻截面Ⅰ-Ⅱ和Ⅲ-Ⅳ誤差絕對值只有2個時刻相等，其余前者均大于后者。通過ΔpⅠ-Ⅱ計算脈動流量誤差上限可達60%，誤差下限非常大可達－100%，甚至差壓為負值導致無法計算;通過ΔpⅢ-Ⅳ計算脈動流量誤差上限可達34%，誤差下限非常大可達－65%。因此減小k1，可有效降低由于遺漏導數項引入的脈動流量計算誤差。

3．4雙路差壓流量計算

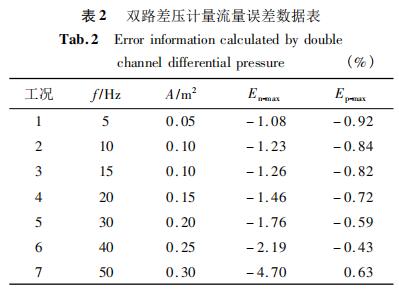
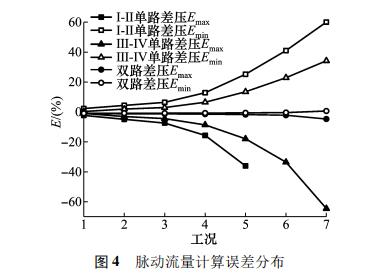
        基于式(8)，利用ΔpⅠ－Ⅱ和ΔpⅢ－Ⅳ計算瞬時脈動流量，表2是雙路差壓脈動流量誤差數據。圖3是工況1和工況7雙路差壓流量計算誤差曲線。圖4是脈動流量計算誤差帶分布。

        通過雙路差壓計算脈動流量，可明顯降低誤差上限，提升誤差下限，使得誤差帶變窄，在高頻率大幅值下尤其顯著。相對于雙路差壓計算流量，通過ΔpⅠ-Ⅱ計算流量的誤差帶寬度非常小，為單路的1/24;通過ΔpⅢ-Ⅳ計算流量的誤差帶寬度非常小，為單路的1/8。

4結論

        研究中針對差壓式流量計測量脈動流量時由導數項引入的計算誤差，提出了采用雙路差壓消除導數項的計算方法，并以文丘里管為研究對象利用流體仿真進行驗證分析，得到以下幾方面結論:

        1)通過單路差壓采用穩態流量公式計算脈動流量，由于遺漏流量導數項分量，造成很大影響，誤差極值可達100%，測量誤差帶覆蓋－100%～+60%，甚至由于差壓為負值而無法進行計算。

        2)通過雙路差壓建立的微分方程組可有效消除導數項影響，脈動流量計算誤差極值為4．7%，誤差帶分布覆蓋－4．7%～0．6%，誤差帶明顯收攏。

        3)建議對雙路差壓計算脈動流量方法在理論和試驗方面進行進一步深入研究，驗證該方法的有效性和可行性。

 

友情提示：感謝本文的作者分享，本文一切觀點都來自于本文作者。